押さえておきたい法則を「力学」を中心に雑多に書き連ねました。
たまに勉強するといろんな分野に関わっている物理
万有引力
F=Gm1m2/r2
G:万有引力定数
相互の物体の質量m1m2と距離rによって決まります。
この式のパターンはあらゆるところで似てきます。
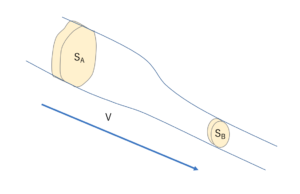
重心
重心は物体を2点で吊るして垂直に下ろした線分の交点です。
立体においては高さの半分の点における輪切りの平面を上記の方法で検証すると重心が求まります。
重心の高さは高いほど倒れ始める角度θは小さくなります。
よって地震対策には背の高いものは低くしなければなりません。
重力による位置エネルギー=mgh
人間の場合はざっくりいえばパーツに分けて総和にします。
力の方向とモーメント
力の支点に対して力点の距離が遠いとより支えるために力がいります。
よって腕で何かを持つ際には体幹部が支点となりますので
体に寄せてから持ち上げないと腕の力は大きくなってしまいますし
体への作用はまた大きくなります。つまり腰への負荷も増すわけです。
滑車の原理
足の牽引などはこれを利用しています。
力の方向を変えているわけです。
足を滑車方向にFの力で引くと、滑車を利用しした方向に力が変わりF=mgの力となるわけです。
つまり足を引く力はつける重りに重力加速度9.8を掛けて計算されなければなりません。
遠心力
F=mv2/r
v:物体の速度 m:物体の質量 r:半径
遠心力(円の中心から離れる方向)=加速度(円の中心に向かって生じる) です
これは遠心分離機における計算で使われます。
速さが2倍なら遠心力は4倍になります。
つまりvが同じでも半径rが大きければ遠心力は小さくなります。
摩擦力
F=μX X:垂直な力(体重) μ:摩擦力
患者をシーツごと滑らせようとすると、シーツとシーツ下部の間にしいているマットとの間に摩擦力が生じます。
スライドパッドなどはおもて面が細かな模様がありますね。これはでこぼこにすることで患者との接地面を少なくしたほうが摩擦力が少なくなるので楽にうごかせるようになります。
(管における)連続の式
vS=constant(一定)
vSρ=constant
v:速度 S:断面積 ρ:密度
管におけるある部分での輪切りにおける領域に流れた量を速さと掛けた場合
その管の径が変わっても連続していれば中に流れる体積は変わらないとうものです。
断面積が小さいほど速度が速いといえます。
それと関連し重要なのが次の定理です。
トリチェリの定理
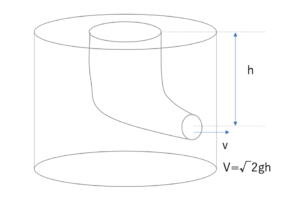
容器の中の液体が,壁にあけた小さな穴から流出するとき,
液体の粘性を無視すれば,流出速度の大きさは
( g は重力加速度,h は穴から液面までの高さ) で与えられる。
P+ρgh+ρv2/2=constant
P:位置エネルギー ρgh:位置エネルギー2 ρv2/2:運動エネルギー
流体の単位体積あたりの質量を表します。
この時v=√2gh(ベルヌーイの定理)と表すことができます。
カテーテルによる血圧の測定はこの原理を利用しています。
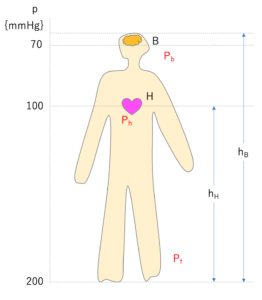
また血圧の部位による変化も似たようなことで考えられます。
Pf=Ph+ρghH=Pb++ρghB
Pf:足(基準)
つまりはエネルギーの保存なのです。
点滴の高さについても同様です。
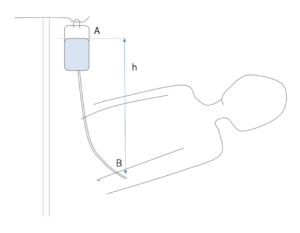
ρgh=1/2ρv2(流体が流れることによる圧力)
=15mmHg(成人静脈洞圧)
=20cm(20cmH2O)
(v=√2ghより)
hが20cm以上ないと逆流するということです。
もっとも実践的とされるのがニュートン流体です。
これは流れというものは栓流ではないだろうとした考えです。
流体力学についてはまた別記事でお話ししたいと思います。
ハーゲン・ポアズイユの法則
流量Q=πa4ΔP/8lμ
このとき
ΔPはP1(円管の手前の圧力)-P2(円管の最後の方の圧力)です。
l:円管の長さ(m)
μ:粘性係数(Pa・s)
これは半径がa, 長さがIの円管を通して粘性のある流体が一定時間内に流れる量Qの関係を表したものです。
これが論文等にも用いられる実践的な流量計算の式といえるでしょう。
これは層流である、円管であることが前提となります。
ちなみに圧力損失ΔPで整理すると下記のようになる
ΔP=8μlv / a2 (v:流速m/s)
インジェクターの注入筒を圧力0:P1とし、刺入点をP2とすれば
粘性が高いほど圧が高い
円管が長いほど圧が高い
流速が早いほど圧が高い
円管半径が大きいほど圧力は低い
ということになります
しかし粘性や流速、円管半径は変化の幅が小さく、円管長が最も大きなファクターになり得ると思われます。
たくさんの物理法則がありますが多くは感覚によって共有することが多いはず。
デバイスもわざわざ式を思い描かなくても感覚で扱えるよう研ぎ澄まされている。
ただ、詳細な検討をするときはやっぱり基本の式に立ち返るとハッとするし
日常にも生きたりする。
物理の式を書いていると、ひとつ実験でもやる気になる。
技師ならではかな。
おしまい。



