母分散未知の場合の解析方法の選択フロー
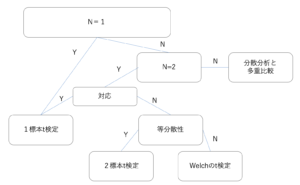
今回は母分散がわからないときの解析について勉強していきます。
母分散がわからないっていうのは、データがどんな分布かわからないってことです。
1標本t検定 とは
・母集団の標準偏差σが未知であり、平均値μ0(母平均:例として、論文等で明らかになっている正常集団の平均値)が既知である
・母集団より無作為抽出する
・標本数、平均値、分散が明らかである
・それらから元の母集団を推測する
例題
研究の目的:
Alを含む制酸剤を投与された乳児の血清Al値は,一般乳児の母平均4.13μg/Lに比べて高値か?
Step1:対立仮説(これから検証したいこと):μ > 4.13 μg/L
帰無仮説(反証): μ ≤ 4.13 μg/L
Step2:乳児10例を対象にデータ収集.
(データ収集により得られた)標本平均:X ̅=37.20 μg/L
(データ収集により得られた)標本標準偏差s: 7.13 μg/L
Step3:検定統計量の算出.
Z=(X ̅-μ0)/(σ/√n)= (37.20-4.13)/(σ/√10)
(ここで母標準偏差σが分からない場合)
→ この時は、標本標準偏差で代用する
標本標本偏差sに置き換えることで、正規分布ではなくt分布に従うようになる
検定統計量: T=(X ̅-μ0)/(s/√n)= (37.20-4.13)/(7.13/√10)=14.67
Step4:p値 Pr(T>14.67) の算出.
検定統計量Tは,自由度(n-1=10-1=)9のt分布に従う.
t分布表
| 自由度 | α=0.1 | α=0.05 | α=0.025 | α=0.01 | α=0.005 |
| 1 | 3.078 | 6.314 | 12.706 | 31.821 | 63.657 |
| 2 | 1.886 | 2.92 | 4.303 | 6.965 | 9.925 |
| 3 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 |
| 4 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 |
| 5 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 |
| 6 | 1.44 | 1.943 | 2.447 | 3.143 | 3.707 |
| 7 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 |
| 8 | 1.397 | 1.86 | 2.306 | 2.896 | 3.355 |
| 9 | 1.383 | 1.833 | 2.262 | 2.821 | 3.25 |
| 10 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 |
| 11 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 |
| 12 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 |
| 13 | 1.35 | 1.771 | 2.16 | 2.65 | 3.012 |
| 14 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 |
| 15 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 |
| 16 | 1.337 | 1.746 | 2.12 | 2.583 | 2.921 |
| 17 | 1.333 | 1.74 | 2.11 | 2.567 | 2.898 |
| 18 | 1.33 | 1.734 | 2.101 | 2.552 | 2.878 |
| 19 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 |
| 20 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 |
| 21 | 1.323 | 1.721 | 2.08 | 2.518 | 2.831 |
| 22 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 |
| 23 | 1.319 | 1.714 | 2.069 | 2.5 | 2.807 |
| 24 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 |
| 25 | 1.316 | 1.708 | 2.06 | 2.485 | 2.787 |
| 26 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 |
| 27 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 |
| 28 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 |
| 29 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 |
| 30 | 1.31 | 1.697 | 2.042 | 2.457 | 2.75 |
| 40 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 |
| 60 | 1.296 | 1.671 | 2 | 2.39 | 2.66 |
| 80 | 1.292 | 1.664 | 1.99 | 2.374 | 2.639 |
| 120 | 1.289 | 1.658 | 1.98 | 2.358 | 2.617 |
| 180 | 1.286 | 1.653 | 1.973 | 2.347 | 2.603 |
| 240 | 1.285 | 1.651 | 1.97 | 2.342 | 2.596 |
| ∞ | 1.258 | 1.645 | 1.96 | 2.326 | 2.576 |
Pr(T>14.67)=6.841e-8 となる。
t分布とは?
正規分布と同様に,単峰かつ左右対称な連続分布
標準正規分布に比べて自由度(degree of freedom:df)が小さいほど分布の裾が重い.
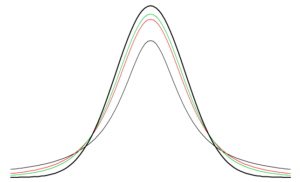
黒:標準正規分布(df=∞のt分布)
緑:df=5のt分布
赤:df=2のt分布
灰:df=1のt分布(コーシー分布)
自由度が大きいと標準に近づく
データ数 ー パラメター数=自由度
次にXの母平均μXに関する95%信頼区間を構成
Pr(X ̅-a ≤ μX ≤ X ̅+a)=0.95
⟺Pr(-a ≤ X ̅-μX ≤ a)=0.95
⟺Pr(-a/(s/√n) ≤ (X ̅-μX)/(s/√n) ≤ a/(s/√n))=0.95
統計量 t=(X ̅-μX)/(s/√n) は自由度 (n-1)のt分布に従う
標本平均:X ̅=37.20μg/L,
標本標準偏差:s= 7.13μg/L より,
a=tϕ (0.975)×s/√n = 2.262×7.13/√10=5.100
*0.975の数字はどこからきたのか?という人へ
→95%信頼区間を求めるにあたり、両端2.5%の値を求めました。
よって検定統計量を見る際には片側だけ見るので、100%(1.0)から引いて97.5%(0.975)です。2.5%(P=0.025をt分布表で、自由度が合うところを見てtの値を求めます。
*そもそもこのaの式はどこから来たのかという人へ
→95%信頼区間の式を両端変形したものです。
*そもそもaってなんだっていう人へ
→平均から95%信頼区間の端までの距離です。
つまり平均ーaと平均+aを合わせると、その範囲は95%信頼区間となります。
母平均μXの95%CI: (37.20-5.10, 37.20+5.10)=(32.10∼42.30)
95%信頼区間は一般の乳児の母平均μ0 4.13μg/Lを被覆しない.
*一般乳児の母平均はμ0、検証に使用した集団の母平均はμX
→母平均という言葉が続いて紛らわしいが別物なので注意
*p値が低いと、95%信頼区間は母平均を被覆しない
→これは1:1の関係である。
Step5(結論):
一般の乳児10名の血清Alの平均値が37.20μg/Lとなることは,極めてまれなこと(p<.0001).
帰無仮説を棄却し,対立仮説を受容するということになる。
『Alを含む制酸剤を投与された乳児の血清Alの母平均の推定値は37.20(95%CI:32.10∼42.30) μg/Lであり,一般の乳児のそれよりも統計学的に有意に高値であることが示唆された(p<.0001).』
2つの標本の仮説検定
・母集団は2つある(はず)
・平均も2つ、分散も2つある(はず)
・2つの母集団は違うものなのか、を検証する
帰無仮説 H0:μX=μY vs. 対立仮説 H1: μX≠μY
*μX=集団Xの平均値、μY=集団Yの平均値
対応あり:2つの標本が同種で対になっている
例)2つの標本が同じ個体から得られている.
治療開始前後の評価.
右左の目に異なる点眼薬を投薬し評価.
クロスオーヴァー試験から得られる評価.
例)双子の兄弟姉妹から得られている.
対応なし:2つの標本は別種
例)2つの標本が別の個体から得られている.
並行群比較試験から得られている.
対応ありの場合
対象:冠状動脈疾患の成人男性63例
評価項目:2回の心運動負荷試験による狭心症発作までの時間の減少率:
標本1:1回目と2回目の間に普通の空気を吸引
標本2:1回目と2回目の間に一酸化炭素を含んだ空気を吸引
仮説:一酸化炭素を含んだ空気を吸引するか否かにより,心運動負荷試験の結果は異なるか?
*対応がある場合は差をとってみる!
→同一個体であれば、差をとる→データが1種類となる→1標本のt検定となる(これはつまるところpaired t testである)
差をとると…
d1 = X1 – Y1
d2 = X2 – Y2
…
d63 = X63 – Y63
新たに差di(i=1,…,63)を標本と考える⇒一標本問題となる
Step1(仮説の構築):
対立仮説(研究の目的): HA: μX ≠ μY⟹ HA : μd ≠ 0 (母集団が離れているということ)
帰無仮説: HA : μX = μY ⟹ HA : μd = 0 (同じものなら相殺されるということ)
差dの母分散は未知⇒t検定(t分布に従わせる)
Step2:冠状動脈疾患の成人男性63例を対象に実験
(データ収集により得られた)標本平均:d ̅=∑63(i=1)di /n = -6.63,
(データ収集により得られた)標本標準偏差sd=√(∑63(i=1)(di – d ̅ )2 /(n-1))= 20.29
*そもそも標準偏差どうやって求めるねんって人へ(式)
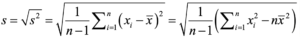
Step3(検定統計量と自由度の算出)
検定統計量:t=(|d ̅– μd |)/(sd/√n)=|-6.63 – 0|/(20.29/√63)=2.59
自由度df:ϕ=n-1=62
*μdがなぜ0になるのか悩む人へ
→分散が等しく、母平均の減算は0になるということ
Step4(p値の算出):
Pr(|T62 |>2.59)=0.0119
*t分布表より
差di = Xi – Yiの母平均μdに関する95%信頼区間を構成
Pr(d ̅-a ≤ μd ≤ d ̅+a)=0.95
⟺Pr(-a ≤ d ̅-μd ≤ a)=0.95
⟺Pr(-a/(s/√n) ≤ (d ̅-μd)/(s/√n) ≤ a/(s/√n))=0.95
統計量 t=(d ̅-μd)/(s/√n) は自由度 (n-1)のt分布に従う
Step2より,
d ̅=(∑63(i=1)di /n=-6.63,
sd=√(∑63(i=1)(di – d ̅ )2 /(n-1))=20.29
ϕ=n-1=63-1=62
⟹ a = tϕ (0.975)×s/√n=1.9990×20.29/√63=5.11
μd の95%CI :(-6.63 – 5.11, -6.63 + 5.11) = (-11.74,-1.52)
信頼係数95%の信頼区間がゼロを被覆しない.
Step5(結論):
減少率の推定値:-6.63(95%CI:-11.74~-1.52)
p値=0.0119.
帰無仮説の下で,このような事が起こることは稀.
帰無仮説(反証)を棄却,対立仮説(研究目的)を受容.
『空気のみを吸った場合の狭心症発症までの時間の減少率と一酸化炭素を含む空気を吸った場合の減少率の差の推定値は-6.63(95%CI:-11.74~-1.52)であり,一酸化炭素を含んだ空気を吸うことにより発症までの時間の減少率が統計学的に有意に短くなることが示唆された(p=0.0119).』
2つの標本が独立な(対応がない)場合
母平均が完全に異なるということ
Step1(仮説の構築):
両側検定:H0 : μX = μY vs. HA: μX ≠ μY
片側検定:H0 : μX ≤(≥) μY vs. HA :μX >(<) μY
Step2(検定統計量と自由度の計算):
t={(X ̅ – Y ̅ ) – (μX – μY )} / √{(sX2)/m+(sY2)/n} ∼ tϕ
分母のばらつきと自由度(degree of freedom: df) ϕ をどう計算するかは,
母集団分布の分散が等しい(等分散: σX2 = σY2 )か?
等しくないか(不等分散: σX2 ≠ σY2 )か? で決まる
*分子はだいたい0になる
→分母:ばらつきは和 どのばらつきであっても結局は含まれてくる
t分布に従う
【独立・等分散な場合】
等分散( σX2 = σY2 )なので,共通の推定値S2 (=SX2 =SY2 )を用いる.
Step3(検定統計量と自由度の計算):
t={(X ̅-Y ̅ ) – (μX-μY )} / √{S2 (1/m + 1/n) } ∼ t(m+n-2)
ただし,
S2={(m-1) SX2+(n-1) SY2} / (m+n-2)
= {∑m(i=1)(Xi-X ̅ )2 + ∑n(i=1)(Yi-Y ̅ )2 } / (m+n-2)
*これらはすなわちstudentのt検定である
→共通のもので括ることができる
例題
対象:健康な子供と嚢胞性線維症を有する子供
評価項目:血清鉄濃度(μmol/L)
研究の目的:嚢胞性線維症を有する子供の平均的な血清鉄濃度は健康な子供のそれと異なるか?
Step1(仮説の構築):
対立仮説:HA :μX ≠ μY(嚢胞性線維症を有する子供と健常な子供の血清鉄濃度の母平均は異なる)
帰無仮説:H0 : μX = μY
Step2(調査・実験):
健康な子供9人:X ̅=18.9, SX=5.9
嚢胞性線維症を有する子供13人: Y ̅=11.9, SY=5.9
2群の母分散は等しいとみなせる.
Step3(検定統計量・共通標本分散の算出)
s2=((m-1) sX2+(n-1) sY2)/(m+n-2)=((9-1) 〖5.9〗2+(13-1) 〖6.3〗2)/(9+13-2)=37.74
t=|(X ̅-Y ̅ )標本平均-(μX-μY )母平均|/√{s2 (1/m+1/n) }標準偏差(共通の推定分散値を使用)
= |(18.9-11.9)-0| / √{37.74(1/9+1/13) }= 2.63
自由度ϕ(df) = m+n-2 = 9+13-2 = 20
*t分布表を見る
0.005 < Pr〖(t20 > 2.63) < 0.010〗
⟹0.01 < p値 < 0.02
母平均の差 μX-μY の95%信頼区間
Pr(X ̅-Y ̅-a ≤ μX-μY ≤ X ̅-Y ̅+a)=0.95
Pr(-a′≤ ((X ̅-Y ̅ )-(μX-μY ))/√(s2 (1/m+1/n) ) ≤a′)=0.95
a′=a/√(s2 (1/m+1/n) )
統計量 t=((X ̅-Y ̅ )-(μX-μY ))/√(s2 (1/m+1/n) ) は自由度m+n-2のt分布に従う.
X ̅-Y ̅=7.0, s2=37.74, ϕ=13+9-2=20
⟹a=2.086×√(s2 (1/m+1/n) )
=2.086×√(37.74(1/9+1/13) )=5.6
*a=tϕ (0.975=t分布表での0.025の値)×√{s2 (1/m+1/n) 『標準偏差(共通の推定分散値を使用)』
μX-μY の95%CI:(1.4∼12.6)
Step5(結果の解釈)
差の推定値: 7.0(95%CI: 1.4~12.6) μmol/L
p値<0.05
帰無仮説(反証)の下で,血清鉄濃度の母平均が 7μmol/Lも異なることは稀である.
帰無仮説(反証)を棄却.対立仮説(研究目的)を受容.
『健康な子供と嚢胞性線維症の子供の血清鉄濃度の母平均の差の推定値は7.0(95%CI: 1.4~12.6) μmol/Lであり,嚢胞性線維症の子供の血清鉄濃度の母平均は統計学的に有意に低いことが示唆された(0.01<p<0.02)』
【独立・不等分散な場合】
プラセボ対照比較試験では,プラセボ群と実薬群で反応が異なり,ばらつきが異なることがある.
そもそも,母分散が分からないため,データに基づき母分散を標本分散で推定している.
そのような状況で,母分散が等しいと仮定することが現実的か?
不等分散を前提とすることが自然と考える人もいる.
(検定統計量と自由度の計算):
t=((X ̅-Y ̅ ) – (μX – μY ))/√((sX2)/m+(sY2)/n)
ϕ=(a+b)2/(a2/(m-1)+b2/(n-1) ),ただし,a=(SX2)/m,b=(SY2)/n
*これらはすなわちWelchのt検定になる
実験をする場合、母分散が正しいという根拠はあるのか?
実薬群とプラセボ群ではしばしば実薬群で分散が大きくなる傾向にある。
なので何も考えずにWelchを選択してもよいかもしれない。
本当に分散が等しければt検定に近づいていく。
例題
対象:60歳以上の孤立性収縮期高血圧症患者
(収縮期160mmHg以上,拡張期90mmHg以下)
評価:研究参加1年後の収縮期血圧
研究の目的:
実薬群の1年後の収縮期血圧はプラセボ群のそれとことなるか?
Step1(仮説の構築):
対立仮説 :HA :μX ≠ μY(実薬群とプラセボ群の収縮期血圧の母平均は異なる)
帰無仮説 :H0 :μX = μY
Step2(実験・調査):
実薬群2308人(m=2308)
収縮期血圧:X ̅=142.5mmHg,標本標準偏差: sX=15.7mmHg
プラセボ群2293人(n=2293)
収縮期血圧: Y ̅=156.5mmHg ,標本標準偏差: sY=17.3mmHg
ただし,2群の母分散は等しいとはみなせない
Step3(検定統計量などの算出):
t=|(X ̅-Y ̅ ) – (μX – μY )|/√(sX2/m+sY2/n)
=|(142.5-156.5)-0|/√(〖15.7〗2/2308+〖17.3〗2/2293)=28.74
*ここでなぜ分子の右辺が0になる?
→結果と仮説の乖離を見てて、分子右辺は仮説下における平均の差
a=〖15.7〗2/2308=0.1068,
b=〖17.3〗2/2293=0.1305
ϕ(d.f.)=(a+b)2/(a2/((m-1) )+b2/((n-1) ))
=(0.1068+0.1305)2/(〖0.1068〗2/((2308-1) )+〖0.1305〗2/((2293-1) ))=4550.6
*自由度はどこから無限大としてとっていいのか?
→t分布表参照
Step4(p値の算出):
*t分布表より
Pr〖(t∞>28.74)<0.005〗
⟹p値<0.01
母平均の差 μX – μY の95%信頼区間
Pr(X ̅-Y ̅-a≤μX – μY≤X ̅-Y ̅+a)=0.95
Pr(-a′≤((X ̅-Y ̅ )-(μX – μY))/√(sX2/m+sY2/n)≤a′)=0.95, a′=a/√(sX2/m+sY2/n)
統計量 t=((X ̅-Y ̅ )-(μX – μY))/√(sX2/m+sY2/n) は自由度ϕのt分布に従う.
X ̅-Y ̅=-14.0, sX=15.7, sY=17.3, m=2308, n=2293, ϕ=4550.6
⟹a=1.960×√(sX2/m+sY2/n)
=1.960×√(〖15.7〗2/2308+〖17.3〗2/2293)=0.955
μX – μY の95%CI:(-15.0∼-13.0)
Step5(結果の解釈):
収縮期血圧の母平均の差の推定値:-14.0(95%CI:-15.0~-13.0)
p値<0.05
帰無仮説の下で,実薬群の1年後の収縮期血圧の母平均がプラセボ群のそれに比べて14mmHg低くなることは稀.
帰無仮説を棄却.対立仮説を受容.
『実薬を服用した被験者の1年後の収縮期血圧の母平均とプラセボを服用した被験者のものとの差の推定値は-14.0(95%CI:-15.0~
-13.0)であり,プラセボに比べ実薬を服用することにより1年後の収縮期血圧の母平均は統計学的に有意に低下する(p<0.01)』
2つ以上の標本の比較
2つ以上の場合どうするか? 対比較をするのか?
(例)運動負荷試験
評価項目:FEV1(努力肺活量測定の最初の1秒間の努力呼気量)
目的:冠状動脈疾患に対する一酸化炭素の暴露の影響が三つの異なる施設で異なるか?
|
Summary of FEV1 |
|||
|
Group |
Mean |
Std Dev |
Freq. |
|
1:JHU |
2.626 |
0.496 |
21 |
|
2:RLA |
3.032 |
0.523 |
16 |
|
3:StL |
2.878 |
0.497 |
23 |
|
Total |
2.831 |
0.521 |
60 |
帰無仮説(反証):μ1 = μ2 = μ3
対立仮説(検証したいこと):帰無仮説が成り立たない
これをひとまず、全てのペアにおいて検証するとなると・・・
2群比較になるように帰無仮説を分離する必要がある.
H0(12) : μ1 = μ2
H0(13) : μ1 = μ3
H0(23) : μ2 = μ3
ここで、いずれかの対比較の検定で H0(ij) : μi = μj が棄却された場合に,
当初の帰無仮説 H0(ij) を棄却
ここで例えば1と2、2と3を比較して大差がない、けれども、1と3を見ると差がある場合には、全体を眺めた時に大差ないように見えるにもかかわらず、差があるという結論に導かれてしまう。式にすると下のようになる。
H0(12): μ1 = μ2 保留
H0(13): μ1 = μ3 棄却 → H0 :μ1 = μ2 = μ3 を 棄却
H0(23): μ2 = μ3 保留
誤って帰無仮説を棄却する(どの群間も=ではないとするということ「実際には=が存在するのに」)確率(第1種の過誤の確率)が増大する
幾つもの条件を何度も繰り返し判断すると,偶然に規準を満たす条件が見つかる.ただ一つの条件を満たしたからOKと判断するのは間違い
そこで全体として包括的に判断する
⇒ 分散分析法
どうしても幾つもの条件を繰り返し判断する必要があり,このような間違いを防ぐためには,個々の条件を厳しくする.
例)対比較の際の検定基準をそれぞれα=1%とすると全体の棄却率としては5%くらいになる。
またその際には多重比較の方法がある。
⇒多重比較法(Bonferroniの方法,Holmの方法,Dunnettの方法,Tukeyの方法など)
実際の第1種の過誤の確率は?
・すべての可能な対比較の検定が独立していると仮定する
・いずれの検定も有意水準5%で検定するとする
例) H012 : μ1 = μ2 , H013 : μ1 = μ3 , H023 : μ2 = μ3
Pr (すべての検定で帰無仮説を棄却しない確率)
= (1-0.05)3=0.857
Pr(少なくとも1つの検定で帰無仮説を棄却する確率)
= 1 – 0.857 = 0.143 > 0.05
これは全てを5%で検定してて棄却を探すと、全体としては14%の確率で間違って棄却してしまう。つまり全体の検定をα=14%でやってるようなものでガバガバの検定である。
これを試しに1%でやるとする。
Pr (すべての検定で帰無仮説を棄却しない確率)
= (1-0.01)3=0.907
Pr(少なくとも1つの検定で帰無仮説を棄却する確率)
= 1 – 0.907 = 0.093 > 0.05
まだ足りない・・・
では0.5%
Pr (すべての検定で帰無仮説を棄却しない確率)
= (1-0.005)3=0.985
Pr(少なくとも1つの検定で帰無仮説を棄却する確率)
= 1 – 0.985 = 0.015 < 0.05
若干のやりすぎ感はある。
一元配置分散分析(One-way Analysis of Variance;ANOVA)
対比較をするから問題が生じる ⇒ 包括的に検定
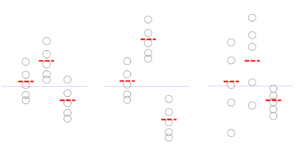
左図1と中央図2の比較: 平均が違いますが、データのバラツキは同じです
左図1と右図3の比較: 平均は同じですが、バラツキが異なります
バラツキが大きいと、赤線の確信度は低いということはわかると思います。
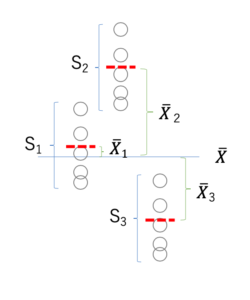
郡内分散と群間分散
群内分散・共通分散 SW2 (この上付きの2は分散なので二乗しているということですね。図では2を省いています)
SW2= ((n1 – 1) s12 + (n2 – 1) s22 + (n3-1) s32) / (n1 + n2 + n3 -3)
群間分散 SB2
SB2=(n1 (X ̅1-X ̅ )2+n2 (X ̅2-X ̅ )2+n3 (X ̅3-X ̅ )2) / (3-1)
もし帰無仮説が正しいならば,SB2 がSW2 に比べて相対的に小さい.
もし対立仮説が正しいならば, SB2 がSW2 に比べて相対的に大きい.
さて、再度運動負荷試験について見てみると
帰無仮説(反証):μ1 = μ2 = μ3
対立仮説(検証したいこと):帰無仮説が成り立たない
が検証用件である。
Step3:統計量の算出
SW2=((n1-1) s12+ (n2-1) s22+(n3-1) s32) / (n1 + n2 + n3-3)
=((21-1) 〖0.496〗2+ (16-1) 〖0.523〗2+ (23-1) 〖0.498〗2) / (21 + 16 + 23 – 3) = 0.254
x ̅=(n1 x ̅1 + n2 x ̅2 + n3 x ̅3) / (n1 + n2 + n3 )
=(21 × 2.63 + 16 × 3.03 + 23 × 2.88) / (21 + 16 + 23) = 2.83
sB2=(n1 (x ̅1-x ̅ )2 + n2 (x ̅2-x ̅ )2 + n3 (x ̅3-x ̅ )2) / (K-1)
=(21 (2.63 – 2.83)2 + 16 (3.03 – 2.83)2 + 23 (2.88 – 2.83)2) / (3-1) = 0.769
F=(sB2) / (sW2 ) = 0.769 / 0.254 = 0.769 / 0.254 = 3.028
Step4:p値の算出
分子の自由度:K-1 = 3-1 = 2
分母の自由度:n-K = 60-3 = 57
0.05 < Pr(F(2,57) > 3.028) <0.10
Step5:結論
三つ施設のFEV1の平均は,それぞれ2.626,3.032,2.878であり,有意水準5%で3群の母平均は統計学的に異なるとはいえず,冠状動脈疾患に対する一酸化炭素の暴露の影響が3施設で異なることは示唆されなかった.
(実際はソフトなどでちゃちゃっとやれてしまうだろう・・・)
ただし、間違えてはいけないのは、間違った方法で対比較をするくらいなら全体を包括的に行いましょうということであり
「=対比較は悪」、ということでは決してない。
対比較:Bonferroni
代表的な対比較法
個々の検定の有意水準を5%以下に設定し,全体して5%とする.
上述した、個々の検定水準を低くして行う、ということと同じことをしている。
帰無仮説 H0 : μ1 = μ2 = … = μk
可能な全ての対比較の回数:(k2)回
α∗=0.05 / 検定回数
Bonferroni法はいかなる状況でも使える万能な方法
⇒ 非常に保守的
(本当は有意差があるにもかかわらず,有意差があると結論付けにくい)な方法.
例) α∗= 0.05/3 = 0.016
運動負荷試験の例でやってみると、
Step1:帰無仮説と対立仮説の設定
対立仮説:H1(i,j): μi ≠ μj
帰無仮説:H0(i,j): μi = μj
Step2:検定統計量 tijを算出
tij=|X ̅i-X ̅j | / √(sw2 (1/ni + 1/nj ) ) (ただし,sw2は共通分散の推定値)
t12=|X ̅1-X ̅2 | / √(sw2 (1/n1 + 1/n2 ) )
= |2.63-3.03| / √(0.254 (1/21 + 1/23) ) = 2.39
Step3: p値の算出.
df = n-k = 60-3 = 57
0.05>Pr (|t12 |>2.39) > 0.02 > 0.05/3
Step4:結果の解釈
:μ1とμ2が等しいという帰無仮説を棄却する十分な根拠は得られなかった.
どんな場合でも使えるが、保守的である
→ 保守的なのが気になる場合はHolmをつかうとよい
対比較:Holm
Step1:全ての比較について検定統計量を算出し,p値を得る
Step2:P値の小さい順に仮説を並べる
Step3:P値の最も小さい比較においては,Bonferroniと同じ基準で検定.
例えば,検定回数がK回ならば,α∗=0.05 / K
Step4:Step3の検定で有意でない場合は検定終了.
検定が有意であった(帰無仮説を棄却できた)場合,検定する仮説の数が1つ減ったので,2番目に小さなp値とα∗=0.05 / (K-1)を比較.
以下,Step4をp値の小さい順に進み,1つずつ分母を減らしながら検定.有意でない比較があれば,そこで検定終了.
つまり、Bonferroniをやって、棄却できるものから棄却して用済みにしていく。一つずつ数を減らして次にとりかかっていくと、段々数が減っていくので楽になっていく。
例) p14=0.001, p13=0.003, p12=0.03, p24=0.031, p23=0.05, p34=0.11
0.001 < 0.05/6=0.0083.H^((14)):μ_1=μ_4を棄却
0.003 < 0.05/5=0.01. H^((13)):μ_1=μ_3を棄却
0.03>0.05/4=0.0125 Stop.
Holm法を改良したShaffer法などもある.
他の多重比較紹介
Tukey法
2群のすべての対比較を行う場合

Dunnett法
1つの対照群との対比較を行う場合
Williams法
単調増加性を改定した1つの対照群との対比較を順次行う場合
などなど,状況に応じて様々な方法が提案.
ノンパラメトリック法に対する方法論もある.
t検定や分散分析のまとめ
データは正規分布に従う.
⇒データ数が十分に大きい場合,t検定でも頑健な結果が得られる.
⇒ノンパラメトリック法:Wilcoxon rank-sum test. Mann-Whitney U test
・2群の分散が等しいことが推測できる
F検定,Leven検定,Bartlet検定 いろいろあるが
Welchのt検定が無難
・多重比較はHolmが無難
昔から多群の試験をやるとき
全体の分散分析をやって、違いがあったら対比較をしていきましょうという考えがあったが、それは昔の話(PCスペックが低いとき)であり、現在はおすすめされない。
今は分散分析より最初から対比較したほうがよい、とされている。
長くかかりました。。。。
おしまい。



